中国期货市场的风险信号识别——基于SMRTT模型的实证检验

一、引言

资产价格的波动变化常常表现出持续的加速上涨并在短时间内瞬间滑落的大幅波动特征，是一个资产价格泡沫的积累与破灭过程。资产价格泡沫的破灭会导致财富的大量蒸发，对于高杠杆的期货投资者来说尤其如此，因此价格泡沫破灭称为期货投资最大的风险。在资产价格泡沫积累和破灭之前进行及时地检验、识别与预警，有助于期货投资者提前采取措施，降低资产价格泡沫破灭带来的冲击影响以及规避可能的财富损失。由此可见，对资产价格泡沫的研究对期货投资者来说具有重要的指导价值。

传统的价格泡沫模型无法反映泡沫反复积累与破灭的非线性特征，也难以区分泡沫与指数增长基本面所对应的高速价格增长（Gürkaynak(2008)）。Lin和Sornette(2013)认为资产价格泡沫不是偏离基本面的更高速的指数膨胀，其本质上是显著快于指数增长的膨胀即超指数增长，超指数增长的过程内蕴着一个临界时点，泡沫在临界时点即表现出发散特征，预示着市场对泡沫的追捧不可能无限持续。然而，临界时点仅仅是理论上的泡沫终结时刻，实际的投机泡沫在接近临界时点积累过程中会越来越不稳定，最终在临界时点之前的某一时刻破裂。基于此，Lin和Sornette(2013)提出了一类新颖的超指数增长泡沫模型——SMRTT模型（Stochastic Mean-Reverting Termination Time）。该模型认为市场投机泡沫积累的过程中，股价会在正反馈机制的作用下呈现超指数增长，内蕴着一个临界时点。SMRTT模型进一步考虑市场噪音交易者、理性投资人的不断进出与信念更新，使得临界时点成为一个随机过程，也不断变化。一旦市场中理性投资人在理性预期下对泡沫的存在性达成了共识，他们即能够对随机临界时点形成一致的无偏估计，即对应为理性预期到潜在的临界时点。同时，理性预期的存在也恰好使得泡沫市场中的临界时点成为一个围绕潜在临界时点做回复振荡的平稳过程。SMRTT模型对泡沫存在性的检验转化为检测一个非线性非平稳股价序列是否蕴含一个均值回复的平稳临界时间序列，并且可以通过估计、表征正反馈强度的指数进行泡沫大小的识别。同时，估计得到的潜在临界时间大小也可以预警泡沫的破灭。

本文试图将这类最新的泡沫模型应用在中国期货市场上，讨论这类模型能否识别中国期货市场中的资产价格泡沫过程，是否能给出价格泡沫准确的风险信号。本文研究了中国期货市场的各类期货的主要产品——沪深300股指期货、黄金期货、基本金属期货中的螺纹钢与铜、能源化工期货中的橡胶、焦炭与塑料和农产品期货中的豆粕、豆油与白糖。实证研究发现，该模型对泡沫过程不仅有非常准确的识别能力，还有较强的预测能力，对于预测资产价格的顶点有着至关重要的作用。

二、模型与方法

（一）SMRTT模型

SMRTT模型的核心假设即认为市场中理性的交易者是序贯进入市场，并且他们一致地意识到了泡沫的存在，认为泡沫理论上会在一个随机的临界时点终结。然而，泡沫的临界时点并不能准确估计，只能得到一个理性预期下泡沫破灭临界时点的无偏估计。这个无偏估计即对应为“潜在临界时点”。而理性预期的存在也客观上使得随机的临界点成为一个以潜在临界时点为无条件期望的“均值回复过程”，以OU过程予以刻划描述。每一个理性投资者依据其进入市场的“风险收益”约束优化自己的退场时间。由于每人所面对的临界时点不同，导致不同的退出时间，这一非同步性实际上即支持了泡沫的延续。

Lin和Sornette(2013)提出的基础模型的假设条件和价格过程如下：

假设价格泡沫破灭之前，股价可以采用如下随机微分方程描述：

其中

它为市场存在泡沫的一个特殊控制因子，代表随机的临界时点，服从OU过程：

上述3式可得到价格p(t)的解析解：

其中

在此基础模型之上，Lin和Sornette(2013)进一步考虑了价格动量的因素，得到了扩展模型，其对数价格y(t)=lnp(t)可用如下过程描述：

其中x代表价格动量，服从如下过程：

进一步假设的过程和、的过程：

在m>2的假设下，Lin和Sornette(2013)得出扩展模型的价格过程：

其中

Lin和Sornette(2013)考察了上述基础模型与扩张模型对US S&P500指数、US NASDAQ复合指数和香港恒生指数的校准，并构建了预警信号。林黎和任若恩(2012)则考察了基础模型对中国上证综指、深圳成指和各行业指数的校准，并构建了对上证综指、深圳成指的预警信号。

（二）校准方法

校准的过程主要是找到合适的价格过程的参数，使得价格过程中所蕴含的随机临界时间序列平稳，同时要求临界时距（潜在临界时点与时间窗口的终点的距离）不能太大。如果存在参数满足上述要求，则发送预警信号。

时间序列是否平稳，通常需要检验序列是否具有确定性的时间趋势和无确定的随机趋势，前者可以用时间序列对时间回归的斜率系数的t检验统计量，后者可以用时间序列的ADF检验统计量。

林黎和任若恩(2012)对模型校准的作法是：采用了禁忌算法，搜索若干组参数，使得时间序列对时间的回归系数的t检验统计量的绝对值最小，然后选择其中一组参数，使得序列的无截距单位根检验统计量最小。而Lin和Sornette(2013)对参数校准的方法不同，他们是先得到10组参数点，使得随机临界时间序列在99.5%的置信水平上拒绝无截距的单位根检验（ADF检验），然后从中选择一组参数，使得时间序列的方差最小。

这类模型的参数校准实际上是一个多目标优化的问题，即找到参数使得随机临界时间序列既不存在时间趋势，也不存在随机趋势。具体而言，就是找到参数使得时间序列对时间回归的t检验统计量的绝对值最小和的无截距单位根检验统计量最小，同时这两个目标函数值满足给定的水平。

然后他们对这种校准过程为多目标优化问题的处理，是将其转化为单目标优化过程，林黎和任若恩(2012)是优化时间序列对时间回归的t检验统计量的绝对值，Lin和Sornette(2013)是优化的无截距单位根检验统计量。因此这两种方法在实际应用时，都可能存在这样一种问题——选择的最有可能不存在时间（随机）趋势的参数点，都可能无法通过随机（时间）趋势的检验。正因如此，对这类模型校准应同时考虑时间序列对时间回归的t检验统计量的绝对值与的无截距单位根检验统计量这2个目标。一种有效的方法是采用散射搜索的方法优化这2个目标的线性组合，另一种方法是采用遗传算法进行多目标优化。

（三）模型的再参数化与参数的限定范围

基础泡沫模型的价格过程可推导出随机临界时间序列为：

从或中，我们也可以看到，在m>1即的情况下，当时间t接近潜在临界时点时（），价格，价格的最大值为K。因此我们对式再参数化：

其中max[p(t)]为给定时间窗口下价格的最大值，因此参数a表示的是泡沫最大化时的价格与当前时间窗口下价格最大值的比例，是泡沫可能程度的标准化度量，不会因为p(t)单位的变化而变化，相对于参数K更具有实际意义。由于泡沫破灭在潜在临界时点前破灭，因此泡沫价格的最大值会大于当前窗口下的价格最大值，从而我们可以设定a>1。我们也可以设定a的上限，在泡沫破灭之前的形成过程中，我们认为泡沫价格的最大值不可能是当前最大价格的5倍或10倍，那么我们可以设定a<5或者a<10。

对式的再参数化，也可以考虑：

这时参数a表示的是泡沫最大化时的价格与当前时间窗口下价格最小值的比例，假设我们认为资产价格泡沫不可能涨20倍，这时我们可以约束参数a<20。

对于基础模型的参数m，我们必须限定m>1以反映股价中体现的正反馈机制，同时还需要限定这种正反馈的程度，比如m<5，避免股价在泡沫形成过程中的走势非常极端。

扩展模型的价格过程可推导出随机临界时间序列为：

从或中，我们也可以看到，在m>2即的情况下，当时间t等于潜在临界时点时，价格，价格的最大值为K。因此我们对式再参数化：

其中a的含义与相同，反映的是泡沫可能的最大程度。我们可以采用类似的方法来约束a。同时我们还需要m的上限以控制价格动量的正反馈程度，比如m<5。从式中有，因此。

（四）泡沫破灭的识别与预测

在实证过程中，我们首先考虑资产价格泡沫识别的问题。本文按照Brée和Joseph(2013)的方法来确定时间窗口的起点和终点，其中终点设置为真实的泡沫破灭时点，而起点为上一次泡沫破灭后至本次泡沫破灭前的价格最低时点。

如何确定真实泡沫破灭时点，Yan, Woodard和Sornette(2012)要求泡沫破灭时点的价格大于前后100个交易日的价格。而Brée和Joseph(2013)则要求泡沫破灭时点的这一价格顶点之前的262个交易日的价格都小于它，并在随后的60个交易日内的价格最低点的价格下跌了25%。我们在这里采用Yan, Woodard和Sornette(2012)的方法来确定，因为第二种方法对期货上市时间的长短和期货历史最高跌幅有更为严格的要求，比如我国的股指期货，由于上市时间比较短，未曾出现过短时间内有25%这么大的跌幅情况，因此采用第二种方法将无法确定任何泡沫破灭时点。

三、实证与分析

（一）股指期货

图 1给出了沪深300股指期货日数据的泡沫起始点和破灭点，根据Yan, Woodard和Sornette(2012)的方法，我们在沪深300股指期货在2010年4月16日至2013年9月30日期间，确定了4个泡沫过程。我们对这4个泡沫过程进行识别，我们首先采用基础模型来识别泡沫过程，通过散射搜索，我们最小化时间趋势t统计量的绝对值和随机趋势的adf统计量，从中选取的标准差最小的几组不同的参数值。我们约束参数a和m小于10，对于基础模型，约束m大于1，而扩展模型则约束m大于2，b大于0。基础模型的校准结果见表 1。

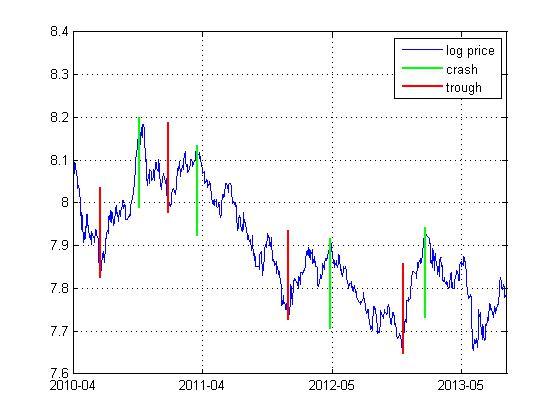
图 1 沪深300股指期货的泡沫起始点与破灭点

表 1的第1列标记的是第几个泡沫过程，第2列（T）为该泡沫过程的窗口长度，第3列为校准参数a，第4列为校准参数m。第5列为临界时距，即潜在临界时点与最近时期的距离；第6列随机临界时间序列的标准差，是Lin和Sornette(2013)在对模型校准时所用到的1个参考标准；第7列为随机临界时间序列的时间趋势t统计量，为林黎和任若恩(2012)在校准时所用到的1个参考标准；第8列为随机临界时间序列的随机趋势adf统计量，是校准模型的重要评判标准。最后两列则给出了时间趋势t统计量和随机趋势adf统计量的临界值。

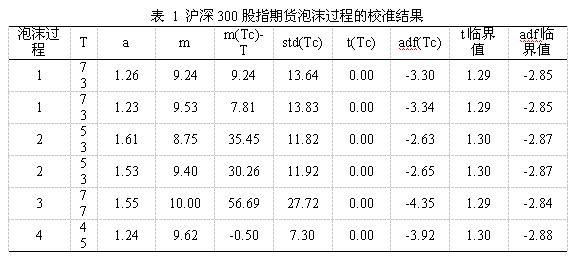    从表 1中我们可以看出，所有的泡沫过程的t统计量都小于对应的临界值，但第2个泡沫模型的adf统计量大于对应的临界值，说明该组参数未能很好地校准模型，泡沫过程无法识别。第3个泡沫过程，校准参数在设定范围的边界上，由于临界时距相对于时间窗口来说也比较大，说明该泡沫过程也未能很好地得到校准。第1和第4个泡沫过程则能得到很好的校准，被准确地识别出来。从未被校准的第2和第3个泡沫过程可以看出，其泡沫过程的破灭点为整个泡沫过程的第2个波峰，由于第1个波峰的资产价格与第2个波峰的资产价格相近，因此我们可以以第1个波峰作为时间窗口的终点，则这两个泡沫过程就能被基础模型所识别出来。

（二）贵金属——黄金

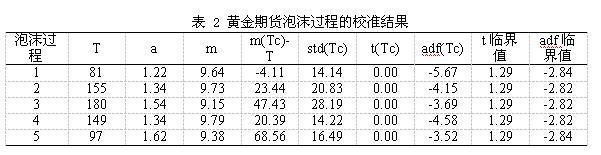
图 2标记了黄金期货日数据的泡沫起始点和破灭点，总共存在5个泡沫过程。表 2给出了各个泡沫过程的校准结果。这里的校准参数均满足t统计量和adf统计量小于对应临界值的要求。从表中的各列信息可以看出，各个泡沫过程都能被基础模型很好地校准，说明基础模型能很好地识别泡沫。不过第5个泡沫过程的校准中，其临界时距相对于时间窗口来说并不小，不过若参照Lin和Sornette(2013)等对临界时距的标准，该临界时距也是满足要求的。

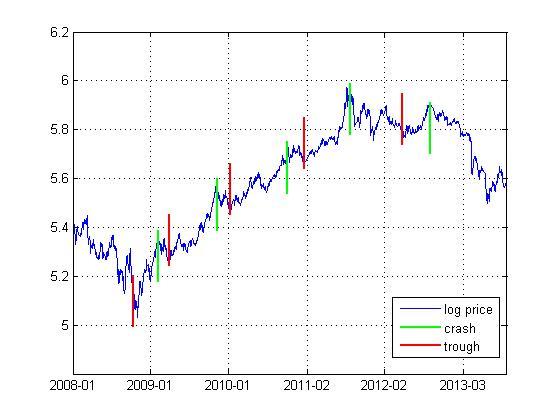
图 2 黄金期货的泡沫起始点与破灭点

（三）基本金属——螺纹钢与铜

表 3列出了基本金属螺纹钢和铜的泡沫过程的校准结果，其中表的上半部分为螺纹钢期货泡沫过程的校准结果，下半部分为铜期货泡沫过程的校准结果。由于铜期货有非常长的历史，它的泡沫过程自然也就更多。

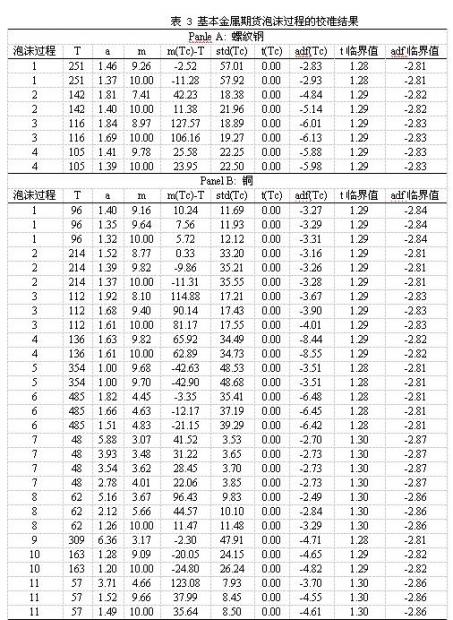
表中对每一个泡沫过程都给出了数组校准参数。我们以铜期货的第1个泡沫过程的校准为例来分析次泡沫过程是否被识别。首先该泡沫过程的3组校准参数使得模型的随机临界时间序列不存在时间趋势和随机趋势，同时临界时距相对于时间窗口来说也非常小，说明这些校准参数是非常合理（模型准确地识别泡沫过程）。其次，我们看到adf统计量和临界时距与参数a和m有着一定的变化规律，即随着a的变小同时m的变大，adf统计量和临界时距有变小的趋势，也就是说，通过设定更低的a和更高的m，我们将得到更为合理的参数，因为更小的a和更大的m预示着更强的泡沫过程。

根据这样一个经验，我们可以认为螺纹钢的4个泡沫过程都能被基础模型准确地识别出来。虽然表中给出的第3个泡沫过程的参数得到的是一个非常大的临界时距，但是我们还是可以进一步搜索到更小的a和更大的m使得临界时距足够小，同时随机临界时间序列的波动也不会非常大。同理，铜期货的所有泡沫过程也是能被基础模型准确地识别。

（四）能源化工——橡胶、焦炭、塑料

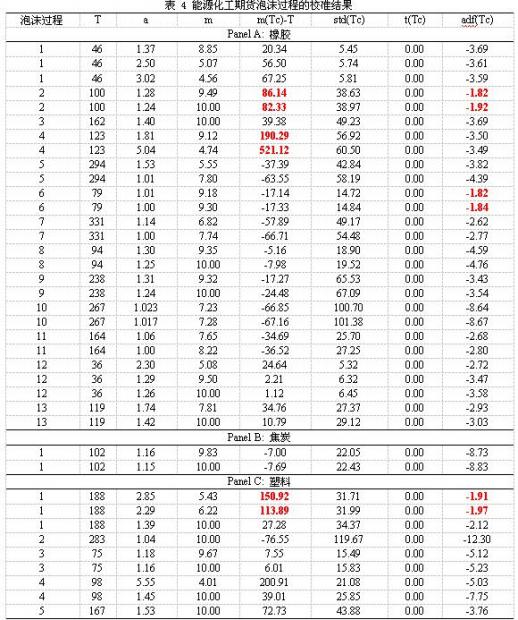
表 4列出了能源化工期货的几种重要产品的泡沫过程的校准结果。表中所列的校准参数（所对应的模型），都预示着泡沫过程的破灭。不过，仍有几组校准的模型的说服力不够，比如橡胶期货的第2个泡沫过程，其校准模型的adf值为-1.92，显著性还不够；橡胶期货的第4个泡沫过程，其校准模型的临界时距相对于时间窗口还太大等等。

如果将模型校准得更有说服力，根据之前的经验，我们只需要搜索更为极端的参数，即更小的a和更大的m。比如对于橡胶的第2个泡沫过程，我们将a的搜索范围设置为[1,1.24]，m的搜索范围为[10,20]，我们的搜索结果是a=1.16，m=19.86，这时模型的adf统计量的值为-3.51，临界时距为34.15，这时模型的adf统计量的值也达到非常高的显著性，同时临界时距相对于时间窗口来说也足够小。其他不够合理的模型都可以通过类似的方式获得更为合理的校准参数，该模型识别泡沫过程的准确性是毋庸置疑的。

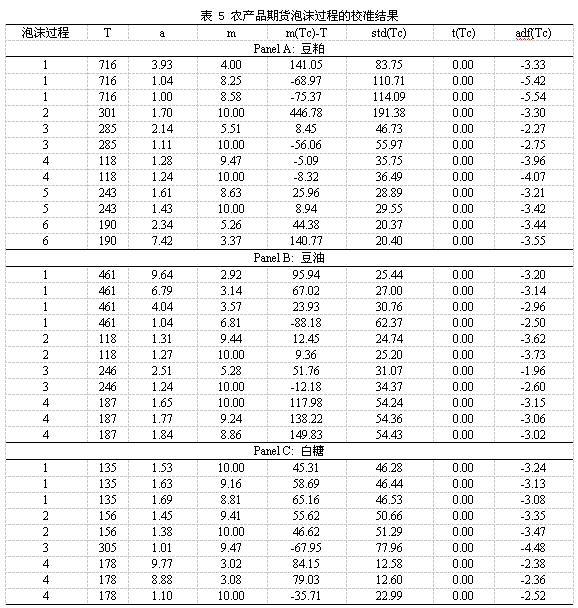
（五）农产品期货——豆粕、豆油、白糖

表 5列出了农产品期货的几种重要产品的泡沫过程的模型校准结果。根据以上的逻辑，所有的泡沫都能被模型所识别。那么进一步，这些泡沫过程是否能提前预测到呢？我们以豆粕期货的第1个泡沫过程为例来展示。图 3给出了豆粕期货的泡沫起始点和破灭点。第1个泡沫过程的时间窗口非常长，有716天。那么我们提前100天能否预测到泡沫过程的破灭了？我们用模型来校准该泡沫过程的前616天的数据，得到参数a=1.1286，m=9.7234，时间序列t统计量的值为0.0000，随机趋势adf统计量的值为-5.5920，临界时距为-27.5743天，这都表明该泡沫过程能提前预测到。

我们还想进一步考察模型会不会错误地预测？我们利用模型来校准第1个泡沫过程的前332个数据，得到参数a=1.8864，m=9.5310，时间序列t统计量的值为0.0000，随机趋势adf统计量的值为-4.3449，但临界时距为484.1283，同时随机临界时间序列的标准差为227.2643，相对于才332天的时间窗口长度，484天的临界时距和227天的标准差都表明在泡沫过程形成的中期都不会预测到泡沫的破灭。

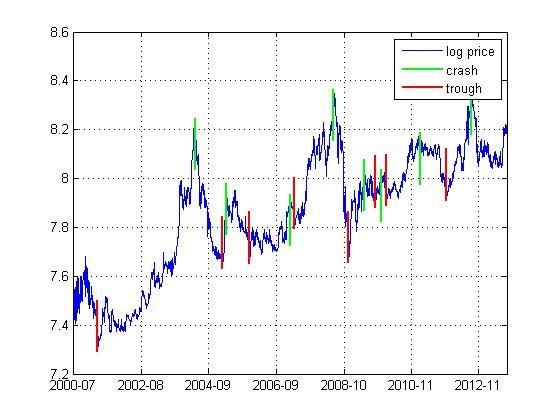
图 3 豆粕期货的泡沫起始点和破灭点

四、结论

本文考察了泡沫模型SMRTT在中国期货市场的应用，重点考察了期货各子类市场的几种成交量最大的产品——股指期货、黄金期货、基本金属（螺纹钢与铜）、能源化工（橡胶、焦炭与塑料）和农产品期货（豆粕、豆油与白糖）。本文的主要贡献可以概括如下：

第一，本文首次系统考察了泡沫模型SMRTT在中国各期货市场主要产品中的应用，不仅证实了该模型对泡沫过程的识别能力，而且证实了它的预测能力。

第二，本文采用了最新的估计方法和时间窗口选择方法，提高了估计过程的有效性，并避免了时间窗口选择的随意性，大大增加了模型的可信性和稳健性。

第三，我们在实证过程中发现，对于一个泡沫过程，模型随机临界时间序列的adf统计量、临界时距这两个关键输出变量与参数a和m有着单调变化的关系，即随着a的变小同时m的变大，adf统计量和临界时距都会变小。这一结论对于模型校准有非常大的帮助。